前の記事を投稿してからだいぶ時間が空いてしまいました。こちらの記事に書いた「データ科学入門Ⅰ」と「データ科学入門Ⅱ」に続いて「データ科学入門Ⅲ」の一部の執筆を担当させていただいているのですが、こちらがなかなか大変で．．．

さて、「データ科学入門Ⅲ」で扱う一つのトピックとして「モデル選択」があります。モデル選択と聞くとおそらく多くの人がAICを頭に思い浮かべるのではないでしょうか。多くの統計解析ソフトがAICの値を出力してくれますし、計算式も非常に単純なので使い勝手が良いので、多くの人が使っているのではないかと思います。ただ逆に使いやすすぎるがゆえに、理論をよく分からずに使っている人も多い印象を受けます。AICを利用する上で、必ずしもAICの導出過程を理解する必要はないかもしれませんが、せめてどのような目的意識でモデル選択をしていることになるかは理解しておいたほうが良いように思います。AICに関して解説している解説論文や記事はたくさんあると思いますが、この記事では数値実験を通じてAICによるモデル選択の意味を解説してみようと思います。

重回帰分析の変数選択

\(n\)組の説明変数と目的変数の組\(D^{n}=((\boldsymbol{x}_{1},y_{1}),\ldots,(\boldsymbol{x}_{n},y_{n})\))が与えられているとします。説明変数は20個あるとしましょう（各\(\boldsymbol{x}_{1},\ldots,\boldsymbol{x}_{n}\)が20次元）。\((\boldsymbol{x}_{1},y_{1}),\ldots,(\boldsymbol{x}_{n},y_{n})\)はi.i.d.で\(p(\boldsymbol{x},y)\)に従うとし、説明変数と目的変数のあいだには線形回帰モデルを仮定しますが、20個の説明変数のうち、どの説明変数が目的変数に対して寄与しているかが分からない状況を想定します。ここでは簡単のため、以下の20個のモデルがモデルの候補であると仮定します。
\begin{align}
m_{1}&: y=\beta_{0}+\beta_{1}x_{1}+\varepsilon\\
m_{2}&: y=\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}+\varepsilon\\
&\vdots\\
m_{20}&: y=\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}+\ldots+\beta_{20}x_{20}+\varepsilon
\end{align}
各変数を含むか含まないかでモデル候補を設定することも多いですが、そうするとモデルの数が\(2^{20}\)個となるので、ここでは簡単のため上記の20個のモデルを候補としています。また簡単のため\(\varepsilon\)は平均0、分散\(\sigma_{\varepsilon}^{2}\)の正規分布に従い、\(\sigma_{\varepsilon}^{2}\)の値は既知であるとします。データ分析者の目的は\(D^{n}\)からモデルおよび回帰係数を推定することです。モデル\(m\)に含まれる回帰係数を\(\boldsymbol{\beta}_{m}\)と表し、\(m\)と\(\boldsymbol{\beta}_{m}\)の推定量をそれぞれ\(\hat{m}, \hat{\boldsymbol{\beta}}_{m}\)と書くことにします。

損失関数と危険関数

\(m, \boldsymbol{\beta}_{m}\)の推定方法を考える上で、どのような推定量が「良い」推定量であるかを考えます。そこでモデル候補の中に\(D^{n}\)を生成していると考えられる真のモデル\(m^{*}\)とそのもとでの真の回帰係数\(\boldsymbol{\beta}^{*}_{m^{*}}\)があると考え、これらに「近い」\(\hat{m}, \hat{\boldsymbol{\beta}}_{\hat{m}}\)が良い推定量だと考えることにしましょう。では\(m^{*}, \boldsymbol{\beta}^{*}_{m^{*}}\)と\(\hat{m}, \hat{\boldsymbol{\beta}}_{\hat{m}}\)の間の「近さ」はどのように計ったらよいでしょうか？これを考える前に、\(m,\boldsymbol{\beta}_{m}\)を推定することは\(p(y|\boldsymbol{x})\)を推定していることになるということを確認しておきます。実際\(m, \boldsymbol{\beta}_{m}\)のもとで
\begin{align}
p(y|\boldsymbol{x},m,\boldsymbol{\beta}_{m})=\frac{1}{\sqrt{2\pi\sigma_{\varepsilon}^{2}}}\exp\left(-\frac{1}{2\sigma_{\varepsilon}^{2}}\left(y-(\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_{d_{m}}x_{d_{m}})\right)^{2}\right)\tag{1}
\end{align}
となります（モデル\(m\)に含まれる最後の変数のインデックスを\(d_{m}\)とおきました）。これにより\(m,\boldsymbol{\beta}_{m}\)のもとでの\((\boldsymbol{x},y)\)の分布が\(p(\boldsymbol{x},y|m,\boldsymbol{\beta}_{m})=p(y|\boldsymbol{x},m,\boldsymbol{\beta}_{m})p(\boldsymbol{x})\)のように定まります。よって\(m^{*}, \boldsymbol{\beta}^{*}_{m^{*}}\)と\(\hat{m}, \hat{\boldsymbol{\beta}}_{\hat{m}}\)の近さを計る方法として、分布\(p(\boldsymbol{x},y|m^{*},\boldsymbol{\beta}^{*}_{m^{*}})\)と分布\(p(\boldsymbol{x},y|\hat{m},\hat{\boldsymbol{\beta}}_{\hat{m}})\)の近さを計るというものが考えられます。分布間の近さを計る尺度にも様々なものがありますが、そのうちの1つにカルバック・ライブラ―（KL）情報量があります。分布\(p(\boldsymbol{x},y|m^{*},\boldsymbol{\beta}^{*}_{m^{*}})\)と分布\(p(\boldsymbol{x},y|\hat{m},\hat{\boldsymbol{\beta}}_{\hat{m}})\)の間のKL情報量は
\begin{align}
\mathrm{KL}(p(\boldsymbol{x},y|m^{*},\boldsymbol{\beta}^{*}_{m^{*}})||p(\boldsymbol{x},y|\hat{m},\hat{\boldsymbol{\beta}}_{\hat{m}}))=\int\int p(\boldsymbol{x},y|m^{*},\boldsymbol{\beta}^{*}_{m^{*}})\log\frac{p(\boldsymbol{x},y|m^{*},\boldsymbol{\beta}^{*}_{m^{*}})}{p(\boldsymbol{x},y|\hat{m},\hat{\boldsymbol{\beta}}_{\hat{m}})}\mathrm{d}\boldsymbol{x}\mathrm{d}y\tag{2}
\end{align}
で定義されます。これができるだけ小さくなるような\(\hat{m},\hat{\boldsymbol{\beta}}_{\hat{m}}\)を求めたいのですが、右辺を展開すると
\begin{align}
\int\int p(\boldsymbol{x},y|m^{*},\boldsymbol{\beta}^{*}_{m^{*}})\log p(\boldsymbol{x},y|m^{*},\boldsymbol{\beta}^{*}_{m^{*}})\mathrm{d}\boldsymbol{x}\mathrm{d}y-\int\int p(\boldsymbol{x},y|m^{*},\boldsymbol{\beta}^{*}_{m^{*}})\log p(\boldsymbol{x},y|\hat{m},\hat{\boldsymbol{\beta}}_{\hat{m}})\mathrm{d}\boldsymbol{x}\mathrm{d}y\tag{3}
\end{align}
となり、第1項は\(\hat{m},\hat{\boldsymbol{\beta}}_{\hat{m}}\)に依存しないので、第2項を最小化すればよいことが分かります。これを\(\hat{m},\hat{\boldsymbol{\beta}}_{\hat{m}}\)に対する損失関数と設定します。
\begin{align}
\ell(m^{*}, \boldsymbol{\beta}^{*}_{m^{*}}, \hat{m}, \hat{\boldsymbol{\beta}}_{\hat{m}})=-\int\int p(\boldsymbol{x},y|m^{*},\boldsymbol{\beta}^{*}_{m^{*}})\log p(\boldsymbol{x},y|\hat{m},\hat{\boldsymbol{\beta}}_{\hat{m}})\mathrm{d}\boldsymbol{x}\mathrm{d}y\tag{4}
\end{align}
ここまでモデルや回帰係数の推定量を\(\hat{m}, \hat{\boldsymbol{\beta}}_{\hat{m}}\)と書いてきましたが、これらは正確には\(D^{n}\)を入力とする関数です。これを明示的に書くと、上記の損失関数は
\begin{align}
\ell(m^{*}, \boldsymbol{\beta}^{*}_{m^{*}}, \hat{m}(D^{n}), \hat{\boldsymbol{\beta}}_{\hat{m}}(D^{n}))=-\int\int p(\boldsymbol{x},y|m^{*},\boldsymbol{\beta}^{*}_{m^{*}})\log p(\boldsymbol{x},y|\hat{m}(D^{n}),\hat{\boldsymbol{\beta}}_{\hat{m}}(D^{n}))\mathrm{d}\boldsymbol{x}\mathrm{d}y\tag{5}
\end{align}
となります。よってこの損失関数の値は\(D^{n}\)の値によってばらつくわけですが、特定の\(D^{n}\)の値に対してだけよい推定量を考えてもあまり意味がありません。そこで損失関数の値を\(D^{n}\)に関して期待値をとった
\begin{align}
R(m^{*}, \boldsymbol{\beta}^{*}_{m^{*}}, \hat{m}, \hat{\boldsymbol{\beta}}_{m})=\mathbb{E}\left[\ell(m^{*}, \boldsymbol{\beta}^{*}_{m^{*}}, \hat{m}(D^{n}), \hat{\boldsymbol{\beta}}_{\hat{m}}(D^{n}))\right]\tag{6}
\end{align}
という量を考えます。ここで期待値は\(D^{n}\)に対して分布\(p(D^{n}|m^{*}, \boldsymbol{\beta}^{*}_{m^{*}})=\prod_{i=1}^{n}p(\boldsymbol{x}_{i},y_{i}|m^{*},\boldsymbol{\beta}^{*}_{m^{*}})\)で取ります。これは統計的決定理論で危険関数とよばれるものに対応します。AICが目指すものの方向性はこの危険関数の最小化です。

最尤推定量の利用と危険関数の推定量

危険関数\(R(m^{*}, \boldsymbol{\beta}^{*}_{m^{*}}, \hat{m}, \hat{\boldsymbol{\beta}}_{\hat{m}})\)を最小化できる\(\hat{m}, \hat{\boldsymbol{\beta}}_{\hat{m}}\)が求められればよいのですが、そもそもこの量は\(m^{*}, \boldsymbol{\beta}^{*}_{m^{*}}\)を知らなければ計算できません。そこでAICによるモデル選択では、この危険関数の推定量を構築して、その推定量を最小化するというアプローチを取ります。そこで、次に危険関数の推定量を考えるのですが、その前に1つステップを挟みます。危険関数\(R(m^{*}, \boldsymbol{\beta}^{*}_{m^{*}}, \hat{m}, \hat{\boldsymbol{\beta}}_{m})\)の最小化では、\(\hat{m}, \hat{\boldsymbol{\beta}}_{\hat{m}}\)両方に関する最小化を考える必要がありますが、この両方の最適化を同時に考えるのは難しいため、AICでは\(\hat{\boldsymbol{\beta}}_{m}\)については最尤推定量\(\hat{\boldsymbol{\beta}}_{m,\mathrm{ML}}\)を使うことにしてしまいます。これによりモデル\(m\)に対する（回帰係数の推定量を最尤推定量に限定した）危険関数は
\begin{align}
R(m^{*}, \boldsymbol{\beta}^{*}_{m^{*}}, m, \hat{\boldsymbol{\beta}}_{m,\mathrm{ML}})=\mathbb{E}\left[\ell(m^{*}, \boldsymbol{\beta}^{*}_{m^{*}}, m, \hat{\boldsymbol{\beta}}_{m,\mathrm{ML}}(D^{n}))\right]\tag{7}
\end{align}
となり、評価基準の最小化をモデルについてのみ行えばよいことになります¹。ただしパラメータの推定量を最尤推定量に限定したとしても、依然としてこの量は\(m^{*}, \boldsymbol{\beta}^{*}_{m^{*}}\)を知らなければ計算できません。先程も述べたように、この量を直接計算するのではなく、この量の推定量を考えて、その推定量を最小化するという方法を考えます。ここは少し天下り的になってしまいますが、(7)式の推定量として
\begin{align}
-\frac{1}{n}\sum_{i=1}^{n}\log p(\boldsymbol{x}_{i}, y_{i}|m, \hat{\boldsymbol{\beta}}_{m,\mathrm{ML}}(D^{n}))+\frac{d_{m}+1}{n}\tag{8}
\end{align}
という量を考えます。この式が幾つかの条件のもとで(7)式の漸近不偏推定量となることが知られており、これを\(2n\)倍したものがAICです。つまり「AICが最小のモデルを選ぶ」ということは「パラメータの推定量を最尤推定量に限定したときの危険関数の漸近不偏推定量の値が最小となるモデルを選ぶ」ということになります。

AICの漸近不偏性を実験で確かめる

さてここからが本記事の本題です。AIC最小化が損失関数をKL情報量としたときの漸近不偏推定量最小化になるということを解説してある教科書や解説文は数多く存在すると思います。ただ、「危険関数の漸近不偏推定量」と言われてもピンと来ない人もいるかもしれません。そこでここでは、この意味を確認するシミュレーション実験を行ってみます。先程のモデル候補\(m_{1},\ldots,m_{20}\)のうち、\(m_{3}\)が真のモデルであるとし、\(y=1+x_{1}+x_{2}+x_{3}+\varepsilon\)が真のモデル（\(D^{n}\)を生成しているモデル）であると仮定します。サンプルサイズ\(n=100\)として(7)式の値（危険関数の値）を\(m_{1}\)から\(m_{20}\)まで変化させて計算してプロットすると以下の図のようになります²。

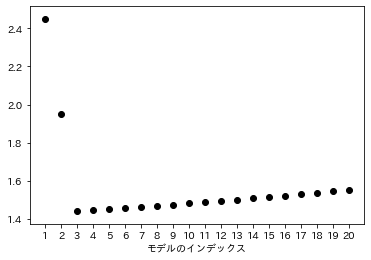
真のモデル\(m^{*}=m_{3}\)で最小値をとっていますが、この計算は真の\(m^{*}\)と真の\(\boldsymbol{\beta}^{*}_{m^{*}}\)を知らなければ計算できません。一方で(8)式はサンプル\(D^{n}\)のみから計算できます。AICの漸近不偏性の意味を理解するために、まず(8)式の第1項を考えます。この項の\(-n\)倍は最大対数尤度ともよばれます。この式の値はサンプル\(D^{n}\)によって決まるので、サンプリングをするごとに異なる値をとります。そこで真のモデルからデータを発生させるというサンプリングを1000回繰り返し、各サンプルに対して(8)式の第1項の値を計算してプロットすると以下の図のようになります。比較のため先程計算した危険関数の値もプロットしておきます。

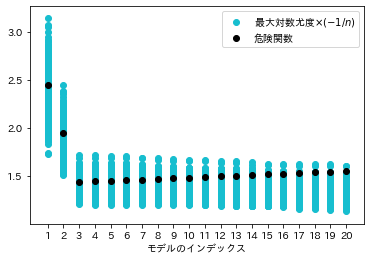
(8)式の第1項の値はサンプルによって異なる値を取るためばらつきますが、重要なのはこの値が危険関数を中心にばらついていないということです。特に変数の多いモデル\(m_{19}\)や\(m_{20}\)においては危険関数の値よりも小さい値を中心にばらついていることが確認できます。そこで(8)式の第2項までを含めた値を改めてプロットすると以下の図のようになります。

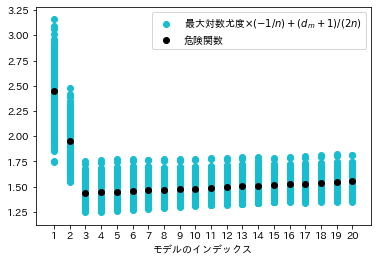
先程とは異なり、(8)式の値は危険関数の値に近い値を中心にばらついていることが確認できます。(8)式が危険関数の漸近不偏推定量であるというのは、サンプルサイズ\(n\)が十分に大きいとき、(8)式が危険関数の値を中心にばらつくということが理論的に保証されるということです。

まとめ

本記事では数値実験を通じてAICによるモデル選択の意味を解説してみました。私自身、学部生時代にモデル選択を卒業研究のテーマにしていたのですが、当時はあまり意味をよく理解していませんでした。今回テキストを執筆するに当たって、記事にあるような実験をしてみたのですが、ちゃんとAIC（の\(\frac{1}{2n}\)倍）が危険関数の中心付近をばらついていて面白いなと思いました。データ分析の論文などを見ると、色々なモデルを構築してその中でAICが最小のモデルを報告するという分析を目にすることも多いのですが、それが分析目的に合致しているのかという点や、ちゃんとAICが危険関数の不偏推定量となる条件を満たしているのかという点に疑問を感じることも少なくありません。AICの導出そのもの（(8)式が危険関数の不偏推定量となることの証明）を理解するのはなかなか骨が折れると思いますが、どのようなことを目標にしているかだけでも理解しておくことは大切かと思います。

1. (6)式では\(\hat{m}\)となっていたものが(7)式では\(m\)となっています。これは(6)式の危険関数は\(\hat{m}\)という関数に対して定義していたのに対し、(7)式は各モデル\(m\)に対して定義された量になっていることによります。(6)式を最小化する\(\hat{m}\)を求めるということは、任意の入力\(D^{n}\)に対する\(\hat{m}\)の出力を求めることになるので、すべての\(m\)に対して定義された危険関数の値を考えて、それを最小化する\(m\)を求めることと同じことになります。
2. (7)式を計算しようとすると\(D^{n}=((\boldsymbol{x}_{1},y_{1}),\ldots,(\boldsymbol{x}_{n},y_{n})\)に関する積分計算が必要になりますが、この数値積分を計算するのは計算量的に難しいため、モンテカルロシミュレーションにより近似的に計算しました。